Kedvenc podcastamben a Gombapresszó-ban feljött a véletlen fogalma. A műsor a megszokott könnyed stílusában a filozófia és matematika mezein szökdelve a fizika 20. százdi eredményeit elutasítva tárgyalta a témát. A mesterséges intelligenciától indulva, a deteminisztikus világképet érintve, a véletlenen időzve, egész a szabad akarat kérdéséig kalandozott. Ez egy 3 órás műsor felében önmagában nem kis teljesítmény. A végkövetkeztetés viszont számomra és Tibi az egyik műsorvezető számára is lehangoló lett, miszerint a világ determinisztikus így a szabad akarat is csak egy ábránd. Erről azért nekem nagyon más emlékeim vannak, de érveim mégse győzték meg Tomit a másik műsorvezető, pedig a kies Déli pályaudvar teraszán sörök mellett volt lehetőségem ecsetelni nézeteimet. Így született meg ez az írás, hogy Tibit felvértezze a következő műsorra a véletlen létezése mellett. Senki se vegye túl komolyan, mert filozófusok és elméleti fizikusok témája ez. Itt meg csak mérnökök győzködik egymást abban az általános hitükben, hogy mindenhez is értenek.
Hétköznapi életünkben véletlenről beszélünk akkor, ha valamit nem tudunk előre megjósolni. Tomi kérdés felvetése arról szólt, ha végtelen kapacitású számítási teljesítmény lenne a birtokunkban, illetve ismernénk a folyamatokat leíró összes egyenletét és azok paramétereit, akkor ki tudnánk e számolni a jövőt.
Fizika területéről lehet olyan példákat hozni, amik jelen tudásunk szerint véletlenszerű események, ilyen például a radioaktív atommagok bomlása, vagy a turbulens áramlás frakterszerű kialakulása, de egy söröző teraszán ezeket, könnyű lesöpörni azzal, hogy a jelenségeket nem ismerjük eléggé, hiszen még a kvantum elmélet sincs egyesítve a relativitás elmélettel. Mérnökök közt nyomós érvek, mivel nem értünk hozzá annyira, hogy meggyőzzük egymást, időnk meg a 11 órás zárás miatt nincs annyi, hogy belevágjunk a két elmélet egyesítésébe.
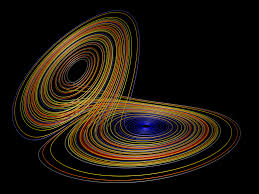
Szerencsére tinédzser korom azon időszakából, mikor még nem múltak el a pattanásaim és az első kondi bérletem sem jártam le, felrémlett egy könyv Káoszelmélet címmel. Ebben szerepelt egy gép a Lorenz kerék vagy Lorenz malóm. Lorenz egy meteorologus volt, aki kezdetleges számítógépen szimulálta egy eszményi bolygó időjárását. Az időjárást meghatározó képletek ugyanis már rég ismertek. Lorenz az eszményi bolygója pontjaihoz hozzárendelte a hőmérséklet, nyomás, páratartalom értékeket, beállította a napsugárzás szögét és ezek mellett az induló paraméterek mellett futtatta a programját. Egészen addig, amíg egy tervezet karbantartás miatt, új gépet kapott, amire a szimulációja minden adatát átmásolta. A régi gépét viszont nem szállították el, így egy darabig a két szimuláció egymás mellett futott. Lorentz, arra lett figyelmes, hogy hetek alatt, kis eltérések jelentek meg az adatokban, majd később a két szimulációban látható időjárás jellegében is eltért egymástól. Program vagy hardver hibára gyanakodott. Azonban kiderült, hogy az eredeti gép néhány tizedes jeggyel többet tárolt a memóriájában, mint amennyi végül átkerült az új programba. Ezek az ezredes nagyságú eltérések okozták azt, hogy a két szimuláció teljesen eltávolodott egymástól, és a közös kiindulásra már nyomokból sem lehetett következtetni.
Pillangó hatásként került be a jelenség a köztudatban. Hiszen Lorentz szimulációjában egy pillangó szárnycsapása által keltett nyomás különbség nagyságrendjéről vagy annál jóval kisebbről beszélünk. A popkulturális mém az, hogy egy pillangó szárnycsapása tornádót kelthet egy másik kontinensen. Valójában én inkább úgy fogalmaznék, hogy egy pillangó szárnycsapásnyi mérési pontatlanság tornádókat rejthet el vagy jelezhet előre hibásan a hosszútávú előrejelzésben.
Lorentz felfedezése után, megindult a kutatás az időjáráshoz hasonló rendszerek keresésében. Ezen rendszerek bár determinisztikusak, tehát matematikai egyenletekkel tökéletesen leírhatóak (nem lineáris egyenlet rendszerekkel), de mégis jövőbeni viselkedésük nem jelezhető előre. Ezt úgy kell értelmezni, hogy adott paraméterek mentén persze a végtelenig számolható, de a paraméterekben felfedezhető bármilyen pici pontatlanság, okozhat bármilyen nagy eltérést. Illetve nem bármilyen nagyot, de mondjuk a rendszer lehetséges állapotain belül két teljesen ellentétes is előállhat ugyanabban az időben, akkor is ha a kiindulás paraméterek eltérése szinte érzékelhetetlen.
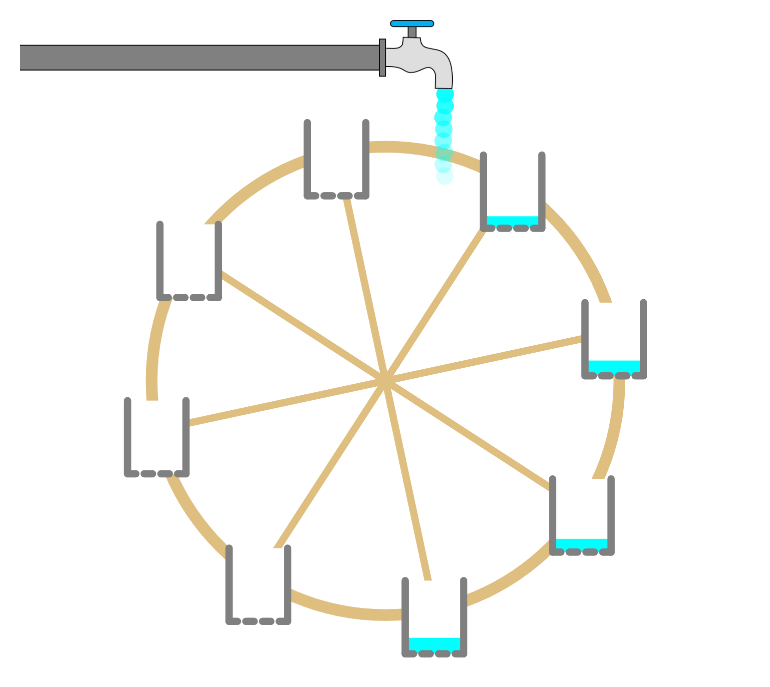
Az ilyen rendszerek megtalálásának akkor van igazán sport értéke, ha a rendszer minél egyszerűbb és egyszerűbb törvényekkel leírható. Egy ilyen egyszerű rendszer a Lorenz kerék vagy malom. Ami egy malomszerűen forgó kerékre függesztett alul lukas vödrökből áll, amire felülről víz folyik. A felső vödör a beömlő víztől telik a többiből pedig a lukon folyik ki a víz. A kerék pedig ettől a súly változástól gyorsul és lassul két irányba, gyakran irányt váltva. Ez a dinamika terepe, tömegek és gravitáció, fel se merülhet senkiben, hogy ne ismernénk eléggé a képleteket.
A következő videóban látható egy ilyen kerék mozgásban. Érdekes megnézni az egészet, de 8:30nál jön a számukra érdekes rész, ahol két kereket indítanak el, köztük ez egyetlen eltérés 0,0004° kiinduló pozícióban van, ez egy 2m átmérőjű kerék esetében a kerületen 0,007 mm eltérést jelentene. 2m es nagyságrendben ez a pontosság talán űrtávcsövek oprikája esetén elképzelhető. Mégis a két kérek nagyon hamar látványosan másképp kezd viselkedni.
A Lorenz keréknél van még egyszerűbb szerkezet, hasonló viselkedéssel. Ez pedig a kettős inga. A kettős inga bemenő paraméterei két tömeg két kar hossz és két indulási szög pozíció. Az alábbi videó azt mutatja meg, mi történik ha csupán az alsó csukló szögén változtatunk.
Számtalan ilyen példát lehet még felhozni, talán a scifi irodalom miatt a háromtest probléma lehet ismert, ami Newton óta fenáll. 3 bolygó mozgása egymás gravitációs terében szinten "kaotikus" tulajdonságokat mutat. Itt kell megjegyezni, hogy a fenti 3 rendszernek is vannak olyan indulási paraméterei melyekkel periodikus mozgást mutatnak.
Hogy jönnek ezek a rendszerek az eredeti vitánkhoz? Ezen rendszerek jövőbeni állapota kiszámítható ugyan, de ha a számítás kiinduló paraméterei végtelenül kicsit eltérést is mutatnak a valóságtól, akkor a számításunk bizonyos idő után az adott rendszer határain belül végtelen nagy tévedést fog mutatni. Én ahhoz, hogy kijelentsem nincs véletlen, azt tartanám szükségesnek, hogy a méréseim ismert pontosságágából az előrejelzésem pontosságára is tudjak következtetni. Newton törvényei szépen leírják a bolygók mozgását, és nem tökéletes mérések alapján is meg tudták határozni a keringési időket és a pályákat. Ezen számítások pontatlansága összemérhető az eredeti mérés pontosságával, és a hiba az idő elteltével "halmozódik" és okoz egyre nagyobb eltérést. Egy kaotikus rendszer esetében, ez nem így van a mérési hiba határból nem tudunk arra következtetni, hogy meddig és milyen pontossággal előrejelezhető a folyamat, sőt lehet, hogy egy nagyobb mérési hiba csak később fog eltérést okozni.
Akinek ez nem elég, mert azt mondja, hogy a mérések lehetnek a mainál sokkal pontosabbak, annak a fizikusok tartogatnak rossz híreket. A mérések pontossága korlátos, egyrészt a megmért részecskével minden esetben kölcsönhatásba lépünk ezzel megváltoztatjuk azt, sőt a kvantum elmélet azt mondja, hogy egyes részecskéket épp a megfigyelő lát el bizonyos tulajdonságokkal, a megfigyelés előtt az univerzum nem ismeri ezeket a tulajdonságokat, ráadásul középiskolás anyag a Határozatlansági reláció amelyik azt mondja ki, hogy bizonyos fizika mennyiségek együtt csak egymással fordított arányban ismerhetők meg, ilyen például az elektron helye és impulzusa.
Tehát tudjuk, hogy a mérésünk nem lehet egy határnál pontosabb, és vannak rendszerek, amik paraméterei végtelenül kicsinek tűnő eltérésre, akár egy elektron tömegére is érzékenyek, így úgy gondolom ezek a rendszerek nem előrejelezhetőek így tekinthetjük véletlennek őket.
A bemutatott rendszerek egyszerű néhány egyenlettel és kiinduló paraméterel leirhatóak: Gondoljunk bele az időjárás, a gazdaság vagy a társadalom folyamatait, hány paraméter írhatja le?
Annak sem kell megrémülni, akit ez a rengeteg vélelten bizonytalansággal tölt el, mert a kaotikus rendszerek is vizsgálhatók sztöchasztikus módszerekkel, pontosan megmondhatók, hogy egy rendszerünk, bizonyos állapotokat, milyen valószínűséggel vesz fel. A kettős inga milyen eséllyel található meg a tér egy szeletében és így tovább. Ha Asimovnak igaza van talán még a társadalmak is jó eséllyel pályára állíthatóak a megfelelő induló paraméterekkel. s
Olvasd el rövid bemutatkozásom és támogass patreonon, hogy podcast és video blog formában is megjelenhessen a blog:https://www.patreon.com/mernokszemme
Facebookon várom a kommenteket, értelmes kérdésekre felvetésekre válaszolok is. A helyesírásom rossz, tudom. Ezt kár megírni, 27 éve hallgatom. Ha eltűnnek a hibák akkor feltörték a profilom. https://www.facebook.com/mernokiszem/





