Szeretnék bemutatni egy gyakorlati példát az elméleti eloszlások alkalmazására. Főleg azoknak, szól akik sosem tanultak hasonlót, szigorúan számítások nélkül. Később ezek megértése szükséges a termék élettartamok vizsgálatához.
Vegyünk egy irodát, ahol 100 ember dolgozik. Ezek az emberek véletlenszerűen kívánnak meg egy kávét a nap folyamán, és mennek a konyhába főzni egyet a közös kávégéphez. Van, aki reggel otthon kávézott, van aki épp elfelejtette, van aki rendszeresen iszik kávét, van aki csak két meeting között. Úgy képzelhetjük el, hogy minden kolléga, minden percben sorsol a fejében egy számot. A 8 órás munka napon 8X60 percében a sorsolt szám percenként 1-480 között mozog, ha a szám 1 vagy 2, akkor kimegy kávézni. Azt tudjuk, hogy egy dolgozó napi átlag 2 kávét iszik meg, mert 480 ilyen kis fejben sorsolásból átlagban kétszer jön ki az 1 és a 2. Így az átlag napi kávék száma 200.
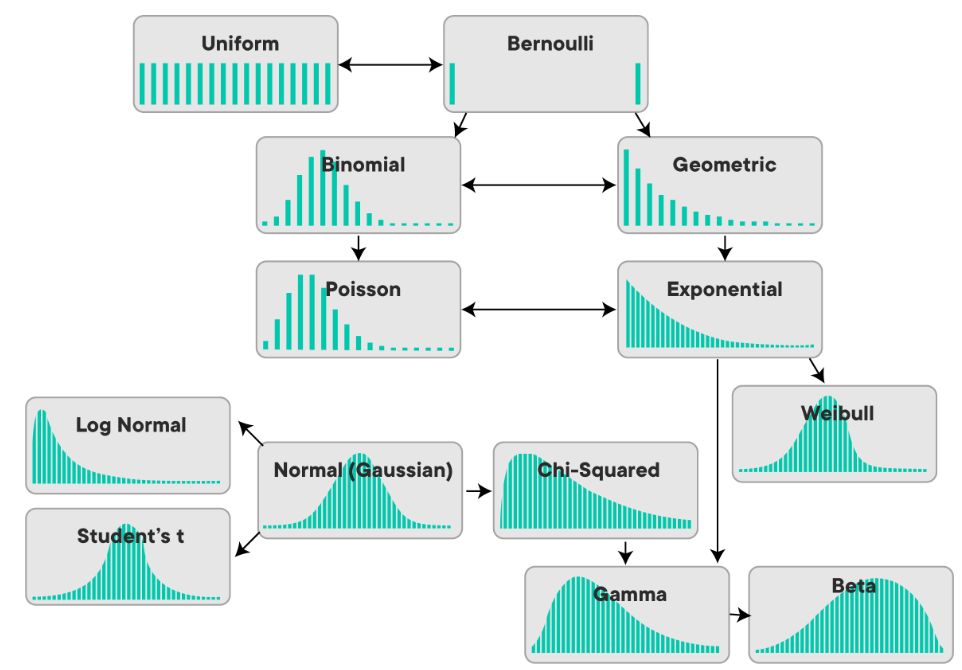
Ebből az alaphelyzetből kiindulva 4 elméleti eloszlást mutatok be.
Binominális eloszlás:
Ez az eloszlás azt mutatja meg, hogy mennyi az esély arra, hogy egy kolléga aznap 0,1,2,3 vagy több kávét iszik. Az elméletben 480 percre és 480 véletlenre osztott világunkban 480 “próbát” végzünk. Egy próba alkalmával a kávézás esélye 2/480=0.00416 Ezt a két számot kell egy kalkulátorban használni, mert a számítással nem akarok senkit sem fárasztani. A következő kalkulátorban https://stattrek.com/online-calculator/binomial.aspx x helyére beírtam sorba a 0 kávé 1 kávét stb
- 0 kávé esélye: 13,5%
- 1 kávé esélye: 27,1%
- 2 kávé esélye: 27,1 %
- 3 kávé esélye: 18%
- 4 kávé esélye: 8,9%
- 5 kávé esélye 3,5%
- 5-nél több kávé esélye: 1,6%
Poisson eloszlás:
A Poisson eloszlás azt mutatja meg, hogy mennyi az esély arra, hogy egy kolléga egy véletlenül kiválasztott időtartamban hányszor megy ki kávézni. Nézzünk egy óra időtartamot. Ehhez azt kell tudnunk, hogy egy nap vagyis 8 óra alatt átlag 2 kávét iszik a kolléga, tehát egy óra alatt 2/8=0,25 kávét átlagosan. A kalkulátor oldalra ezen kívül még a kávé ivások számát kell beírni https://stattrek.com/online-calculator/poisson.aspx . Egy óra alatt a 0,1,2 vagy több kávé esélye:
- 0 kávé esélye: 77,8%
- 1 kávé esélye: 19,4%
- 2 kávé esélye: 2,4 %
- 2-nél több kávé esélye: 0,02%
Poisson és binominális eloszlás összefüggése. Aki kicsit szemfülesebb és követett, az érezheti, hogy ez a két számítási mód felcserélhetőnek tűnik. A megérzés jó, ha kicsi a valószínűség és nagy a minta szám, akkor jó közelítéssel felcserélhető a két számítási módszer. A különbség abból adódik, hogy a binominális eloszlásnál egy óra alatt maximum 60 kávét ihat meg, mert elméletben percenként sorsolunk, míg a poisson esetében nincs szükség erre az elméleti megközelítésre, ott nincs maximuma a kávék számának. A legjobb példa ezt szemléltetni talán az, hogy a Júliusi esős napok számát binominális eloszlás sál számoljuk a júliusi esők számát pedig poissonnal, mert poisson esetében figyelembe vesszük, hogy egy nap több eső is kialakulhat., binominális esetében pedig az esős napok számát keressük, ami napi maximum 1-et havi 31. -et jelent
Exponenciális eloszlás:
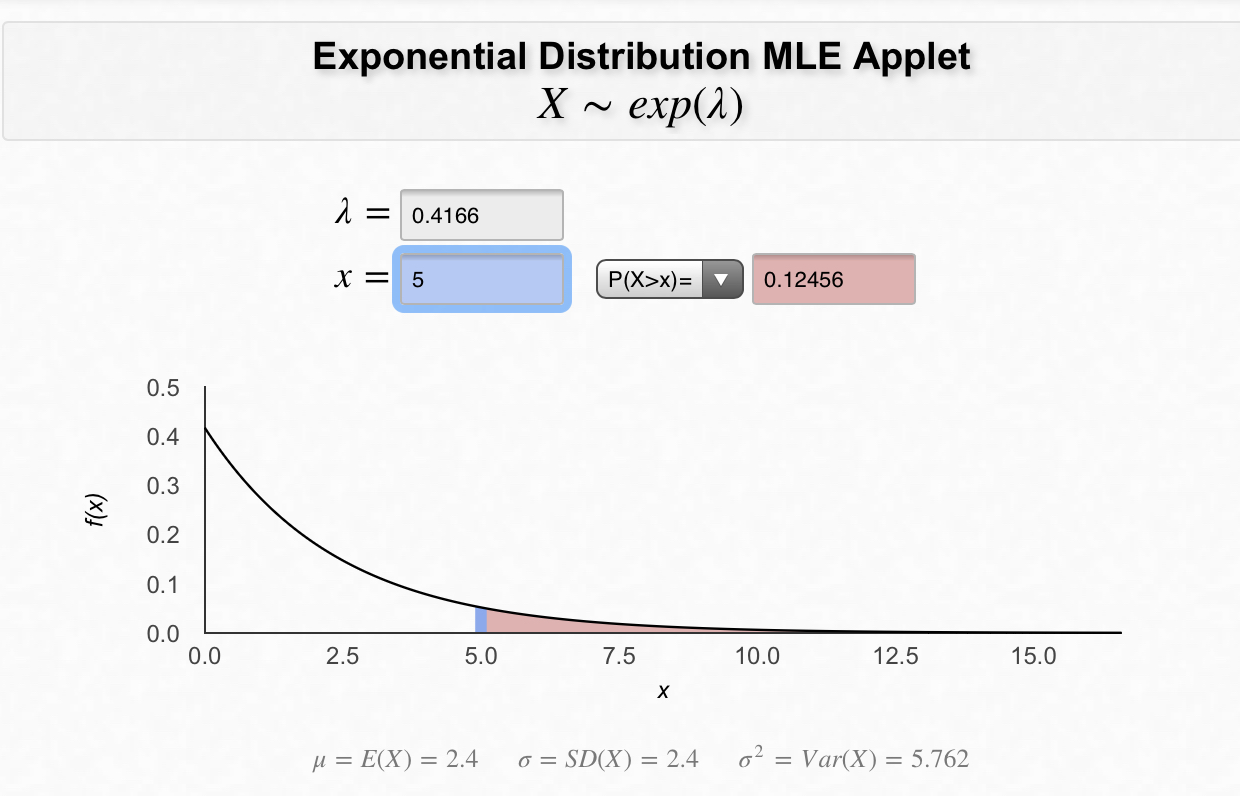
Az exponenciális eloszlás megmutatja, hogy mennyi idő telik el két véletlen esemény között. Arra használhatjuk, hogy megnézzük a képzeletbeli irodákban, mennyi a valószínűsége annak, hogy 5,10,20 percig senki nem megy a kávégéphez. Ehhez ki kell számolnunk a két kávézás között várható időtartamot. Esetünkben 480 perc alatt 200 kávét fogyasztanak átlagban. Így a várható értékünk 2,4 perc. Ennek a reciprokára van szükségünk, ami 1/2,4=0,4166. Egy újabb kalkulátorba beírva(https://homepage.divms.uiowa.edu/~mbognar/applets/exp-like.html) ezt és a vizsgált időtartamokat a következő eredményt kapjuk:
- 5 percig üres a konyha: 12,5%
- 10 percig : 1,6%
- 20 percig : 0,002% ne számítsunk 20 perc magányra a konyhában
A függvény alatti teljes terület a 100%, a piros rész pedig ebből az adott időintervallumnál hosszabbak előfordulásának aránya. Tehát a piros terület aránylik az egészhez.
Az exponenciális eloszlás rendelkezi néhány “Drámai” tulajdonsággal:
- Emlékezet nélküliség. Mindegy melyik időintervallumot vizsgáljuk, sőt az is mindegy, hogy a konyha már éppen 5 perce üres a következő 5 percre mégis a számított érték lesz jellemző.
- Várható érték és a szórás azonos. Esetünkben a 2,4 perc a kávék között eltelt időtartamok számtani átlaga és ezeket az idő tartamokat lemérve a szórásunk is ennyi lesz.
- A várható érték nem a legvalószínűbb érték. A várható értéknél a kávék között mért intervallumok 63,21%-a rövidebb. Ezt ledek esetében pl karakterisztikus élettartamnak nevezzük, és a ledek 63,21%-a hamarabb megy tönkre ennél a várható élettartamnál. Az élettartam számtani átlagánál a medián átlag kisebb. Ezért nem közli a KSH sem a magyar bérek mediánját csak számtani átlagát.
A normális vagy Gauss eloszlás:
A Gauss eloszlás megmutatja a naponta meghívott kávék számának eloszlását. Tudjuk, hogy az átlag napi 200, de mennyi az esély arra, hogy egy nap 220 kávénál több fogy el? A normális eloszlást átlag értékkel és szórással jellemezhetjük. Ezt a legegyszerűbb úgy megkapni, ha napokon keresztül mérjük a az elfogyasztott kávék számát és ezt feljegyezzük, minél több napot mérünk annál megbízhatóbb az eredményünk. Az eddigi paraméterek alapján is meghatározható a kis elméleti irodánk napi kávé fogyasztásának eloszlása (nem tudtam megcsinálni :) de érzem, hogy lehet). A korábban megismert binominális eloszlást használtam a szórás meghatározására. Ehhez meg keresetem, hogy a 100 ember x 480 perc=48000 próba és 2/480 esélye mellett, milyen értéknél nagyobb érték bekövetkezési esélye 15,87%. Ugyanis ebből az értékből az átlagot levonva kapjuk meg a normális eloszlásunk szórását. Akit jobban érdekel, honnan jött a 15,87% az keressen rá a 3 sigma szabályra.
https://keisan.casio.com/exec/system/1180573198
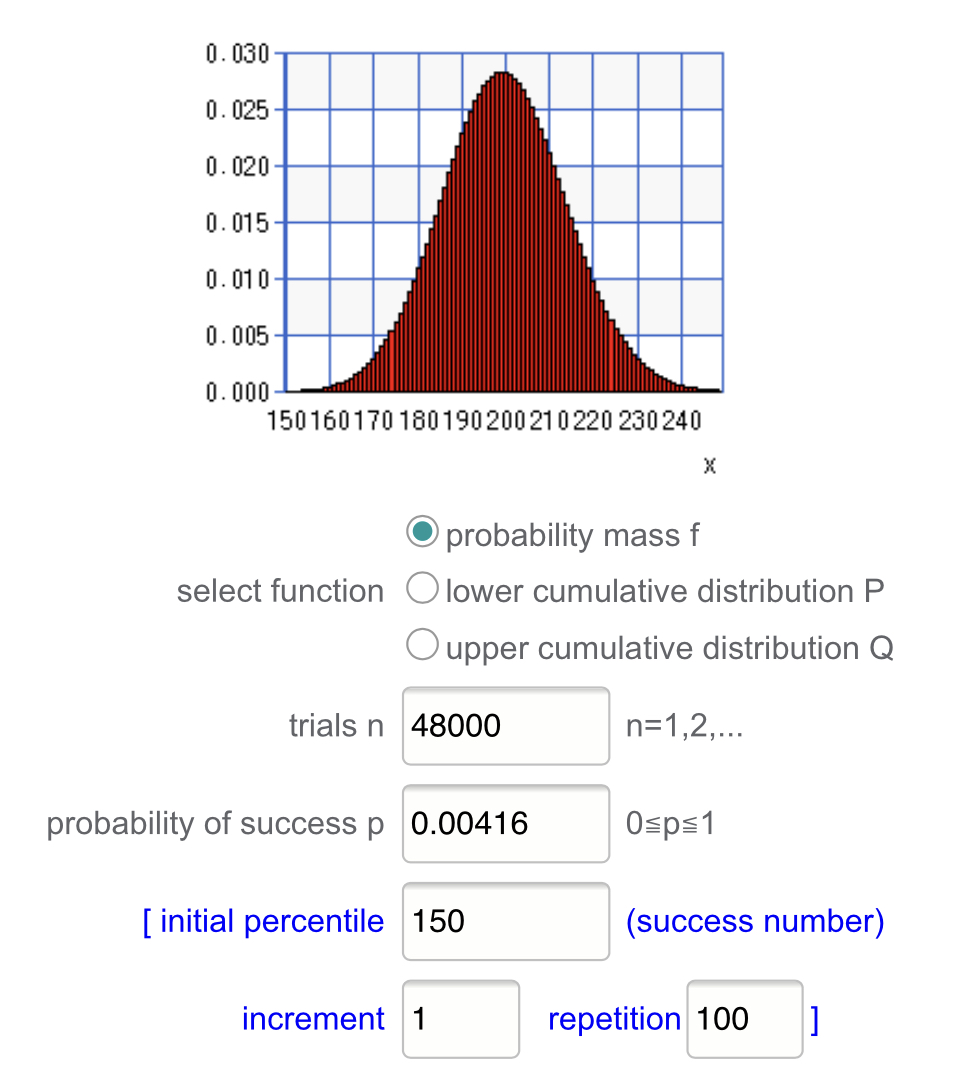
Ilyen szép normális eloszlás haranggörbéjéhez illeszkedő grafikont ad a binominális eloszlásunk. Természetesen nem teljes az illeszkedés, mert a binominális csak természetes számon értelmezető, a normális pedig a valós számokon is.

A keresett szórás közelítve 14. Tehát a normális eloszlásunk átlag értéke 200 és szórása 14. Erre van szükség egy kalkulátorban. https://stattrek.com/online-calculator/normal.aspx 220nál több adag kávé a napok 7,7%-ban fogy.
Ezt a binominális eloszlás kalkulátorával is megkaphattuk volna, de a valóságban gyakrabban ismerünk történelmi adatokat, itt az előző napok kávé fogyását, így jobban könnyebb normális eloszlással számolni.
Remélem más is meglátta ennek a területnek a szépségét. Én BME MBA szakán találkoztam először a valószínűség számítással Dr. Kövesi János tolmácsolásában. A Professzor remek előadásai egy félév alatt olyan hatással voltak rám, hogy szinte mindent ezzel a kvantitatív szemlélettel nézek azóta. Aki kicsit mélyebben érdeklődik az elmélet után, annak a Mateking remek előadásait ajánlom, ahol ez a témakör pont ingyenes: https://www.mateking.hu/valoszinusegszamitas/eloszlas-eloszlasfuggveny-surusegfuggveny
Olvasd el rövid bemutatkozásom és támogass patreonon, hogy podcast és video blog formában is megjelenhessen a blog:https://www.patreon.com/mernokszemme
Facebookon várom a kommenteket, értelmes kérdésekre felvetésekre válaszolok is. A helyesírásom rossz, tudom. Ezt kár megírni, 27 éve hallgatom. Ha eltűnnek a hibák akkor feltörték a profilom. https://www.facebook.com/mernokiszem/





